Matematika s přehledem 4 – Goniometrie
Doplňky
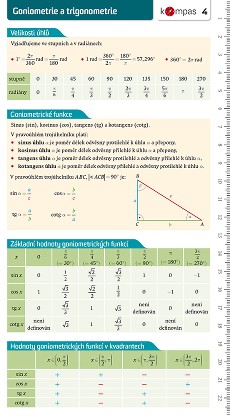
Přehledy vybraných důležitých vzorců a vět středoškolské matematiky - goniometrie a trigonometrie: goniometrické funkce, míra stupňová a oblouková, základní hodnoty goniometrických funkcí, goniometrické vzorce, věty sinová a kosinová.
- ISBN
- K 095
- EAN
- 8594022787961
- Formát
- 127 x 230
- Rok vydání
- 2015 (1. vydání)
-
Běžná cena 10 Kč s DPH
-
Skladem Ne
-
Přihlaste se a nakupte za cenu od 9 Kč s DPH.
Popis
Desetidílný užitečný pomocník při studiu matematiky, vytištěný na tvrdším laminovaném papíru v praktickém formátu oboustranných záložek.
Matematika s přehledem – obsahy jednotlivých dílů 1–10:
- Matematika s přehledem 1 – Základní poznatky: číselné obory, dělitelnost přirozených čísel, intervaly, množinové operace, logika
- Matematika s přehledem 2 – Geometrie: vzorce pro obsahy, obvody, objemy, povrchy, Eukleidovy věty, Pythagorova věta
- Matematika s přehledem 3 – Algebra: mnohočleny, vzorce pro úpravy mnohočlenů, pravidla počítání s mocninami a odmocninami, usměrňování zlomků
- Matematika s přehledem 4 – Goniometrie a trigonometrie: goniometrické funkce, míra stupňová a oblouková, základní hodnoty goniometrických funkcí, goniometrické vzorce, věty sinová a kosinová
- Matematika s přehledem 5 – Posloupnosti a finanční matematika: vlastnosti posloupností, aritmetická a geometrická posloupnost, úroky, inflace, spoření
- Matematika s přehledem 6 – Logaritmy: logaritmické funkce, pravidla pro počítání s logaritmy
- Matematika s přehledem 7 – Kombinatorika: faktoriál, permutace, variace, kombinace, binomická věta
- Matematika s přehledem 8 – Analytická geometrie, kuželosečky I: kružnice, parabola, středové rovnice, vzájemná poloha přímky a kuželosečky, analytické řešení
- Matematika s přehledem 9 – Analytická geometrie, kuželosečky II: elipsa, hyperbola, středové rovnice, vzájemná poloha přímky a kuželosečky, analytické řešení
- Matematika s přehledem 10 – Diferenciální a integrální počet: věty o limitách, důležité limity, pravidla pro derivování, derivace elementárních funkcí, základní vzorce pro primitivní funkce